机器学习

机器学习分类

机器学习分为监督学习和非监督学习。

监督学习：输入数据得到“正确的”输出，输入与输出是映射关系。回归算法（Regression），比如用线性回归来预测房价；分类算法（Classification），比如输入肿瘤信息将其分类为良性、恶性等类别。

非监督学习：输入数据得到的输出没有“正确”的概念，常用于寻找数据中的结构。聚类算法（Clustering），将相似的数据归类在一起；异常检测（Anomaly Detection），找出不寻常的数据；降维（Dimensionality Reduction），将大数据集压缩成小数据集并尽可能减少信息丢失。

线性回归

x -> f -> $\hat{y}$ 。

• x 是输入变量（input variable），又称特征（feature）。
• y 是输出变量（output variable），又称目标变量（target variable），是训练集（training set）中的实际真实值。
• m 是训练样本数，数据集的大小。number of training examples。
• $\hat{y}$ 是模型（model）预测值

$$(x,y) = single \quad training \quad example \\\\ (x^{(i)},y^{(i)}) = i^{th} \quad training \quad example$$

通过训练集训练模型（model），然后给模型输入x，模型输出 $\hat{y}$ 作为预测值。

单输入线性回归（Linear regression with one variable）

$model : f_{w,b}(x) = wx + b$​

w 代表权重（weight），b 代表基础值（base value）。

代价函数

Cost function : Squared error cost function.

$J(w,b) = \frac{1}{2m} \sum\limits_{i=1}^{m}(\hat{y}^{(i)} - y^{(i)})^2 = \frac1{2m} \sum\limits_{i=1}^m(f_{w,b}(x^{(i)}) - y^{(i)})^2$

训练集的代价越小，模型越符合预期。代价函数中的 2 是为了梯度下降中求偏导时使公式更加简洁，因为 J 求偏导时外函数的导数会产生乘 2 ，正好抵消。

梯度下降（Gradient descent algorithm）

用于最小化代价函数的一种算法。参考不至于吧，梯度下降简单得有点离谱了啊。

$$w = w - \alpha \frac{\partial}{\partial w} J(w,b) \\\\ b = b - \alpha \frac{\partial}{\partial b} J(w,b)$$

其中，α 代表学习率，用于控制步长，防止步长过大导致 J 在最小值附近反复横跳而无法收敛。因此学习率的合适取值很重要。

偏导则作为方向以及基本步长。梯度是偏导数构成的向量。

多元线性回归（Multiple linear regression）

注：不是多元回归（Multivariate regression）。

$$x_j = j^{th}feature \\ n = number \quad of \quad features \\ \vec x^{(i)} = features \quad of \quad i^{th} \quad training \quad example \\ x^{(i)}_j = value \quad of \quad feature \quad j \quad in \quad i^{th} \quad training \quad example$$

现引入多个特征值x，每个x的下标不同。每个特征值都有对应的权重。

$$f_{\vec w,b}(\vec x) = w_1x_1 + w_2x_2 + ... + w_nx_n + b = \vec w \cdot \vec x + b \\ \vec w = [w_1 \quad w_2 \quad ... \quad w_n] \\ \vec x = [x_1 \quad x_2 \quad ... \quad x_n]$$

向量化

在 python 中，我们常使用 numpy 库来进行科学计算。

通过np.array()初始化一维数组，通过np.dot()方法调用点乘运算。点乘方法比单纯的循环遍历相乘之和更加快速，特别是数据量大的情况下，因为 numpy 方法可以使用一些硬件来实现加速计算，比如分成多个部分并行计算？这比单纯的循环或许快上许多。

w = np.array([1.0, 2.0, 3.0])
x = np.array([10, 20, 30])
b = 2
# 通过点乘的方式来简化运算
f = np.dot(w,x) + b

特征缩放

在使用梯度下降求解模型参数以最小化代价函数时，有时因为不同参数的取值范围不同，特别是一个范围特别大，一个范围特别小的情况下，会导致不同参数在各自方向上的下降步子相差较大。如果说梯度下降最好的情况是不同方向上的步子一致，经过合成后迈出的一步刚好是去往最低点的方向，那么上面提到的情况就是走得有点斜，相比较之下就是饶了圈子，虽然也能到达最低点，但是由于走的距离变长，需要的步子也就变多，即迭代次数变多。如下图所示，较优的是步子较少的路线，绕远路的则是较差路线。

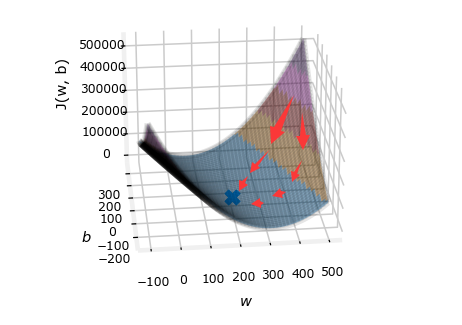
为了尽可能减少迭代次数，通过“特征缩放”可以协调不同方向上的下降距离，以优化梯度下降。而特征缩放的做法就是：对数据集的各个特征值进行处理，使得不同的特征具有相似的取值范围。下面有两种简单方法。

1. 均值归一化（Mean normalization）：$x_i = \frac {x_i - \mu_i} {x_{max} - x_{min}}$，其中 μ 代表某个特征中的平均值，这是缩放到 0 的周围。
2. 最小-最大值归一化（min-max normalization）：$x_i = \frac {x_i - x_{min}} {x_{max} - x_{min}}$，这是缩放到 [0,1] 区间。